> Energy band gap>
GaAs |
AlxGa1-xAs |
InxGa1-xAs
> Refractive index
> GaAs |
AlAs |
AlxGa1-xAs |
InxGa1-xAs
> Devices
> Bragg mirror |
SAM |
RSAM |
SA |
SANOS |
SOC |
Microchip |
PCA
> Device application
> Papers |
Patents |
FAQs

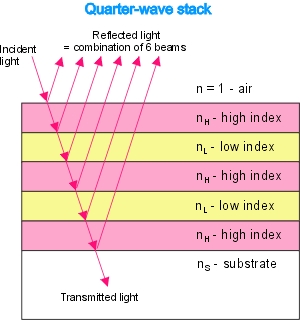
Bragg mirror
Construction of a Bragg mirror
A thin film Bragg reflector consists of a multilayer-stack of alternate high- and
low-index films, all one quarter wavelength thick (see figure right).
The geometrical thicknesses of the high- und low-index films are
tH = λ/(4nH) and
tL = λ/(4nL) respectively.
nH and nL are the indices of refraction of the high- and
low-index films, respectively and λ is
the center wavelength of the Bragg mirror.
On every interface in the stack a part of the incident beam is reflected.
The reflected parts have a phase shift of 180° only if the incident light
goes from low-index medium in a high-index medium. The relative phase difference
of all reflected beams is zero or a multiple of 360° and therefore they interfere
constructively.
The intensity of the incident light beam decreases during his travel trough
the quarter-wave stack and at the same time the reflected light increases, if
the absorptance A of the stack is negligible.
• Reflectance
Reflectance of a Bragg mirror
The reflectance R of a quarter-wave stack in air or free space with high-index layers outermost on both sides is given by :
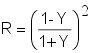
with
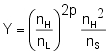
- Y - admittance of a quarter wave stack with (2p + 1) layers
- nH - high index of refraction
- nL -low index of refraction
- nS - index of the substrate
- (2p + 1) - number of layers in the stack
Approximation
If the number (2p + 1) of films in the quarter-wave stack is large and the absorption can be neglected then the reflectance R and the transmittance T can be approximated by
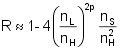
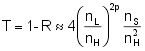
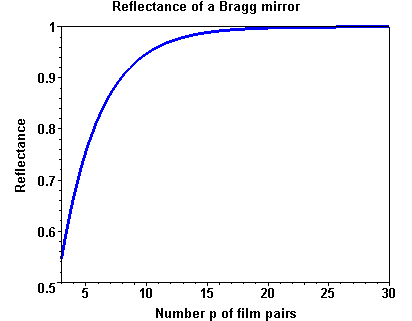
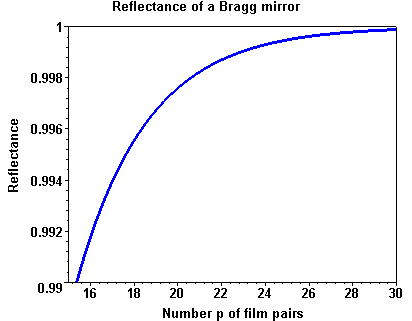
Numeric examples
Reflectance of a Bragg mirror as a function of the number p of film pairs with nH = nS = 3.5 and nL = 3.0.
• Spectral width
Spectral width of the high refletion zone
The spectral width Δλ of the high reflectance zone increases with increasing
difference of the refractive indices nH - nL.
Δλ can be estimated with the design wavelength λ0 of the quarter-wave stack by
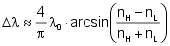
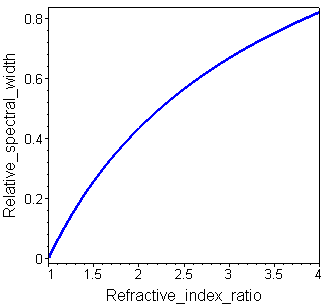
The relative spectral width w = Δλ/λ of the high reflectance zone as a function of the ratio of the refractive indices nH/nL is shown in the figure right.
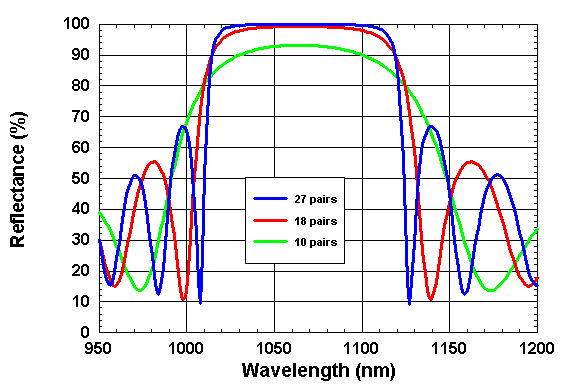
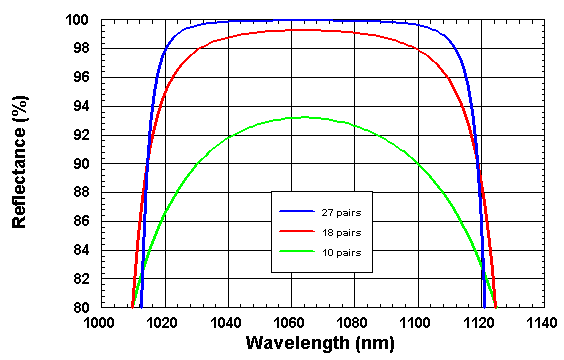
• AlAs/GaAs Bragg mirror
AlAs/GaAs Bragg mirror
For the wavelength 1064 nm the refractive indices
of the materials GaAs and AlAs are n(GaAs) = 3.49 and n(AlAs) = 2.95, respectively.
The figures below show the spectral reflactance of AlAs/GaAs quarter-wave stacks with the center wavelength
The figures below show the spectral reflactance of AlAs/GaAs quarter-wave stacks with the center wavelength
λ0 = 1064 nm and different numbers of AlAs/GaAs pairs.